二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。

二叉树的遍历方式有很多，但是如果限制从左往右的方式，则主要分为四种：

1. 前序遍历
2. 中序遍历
3. 后序遍历
4. 层序遍历

前序遍历

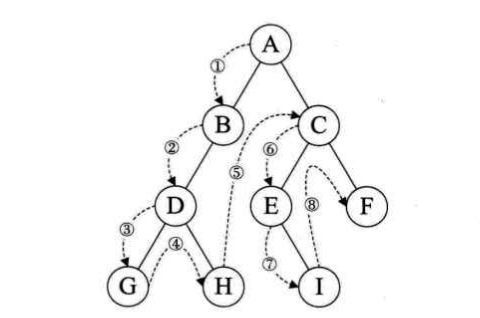
规则：若二叉树为空，则空操作返回；否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。如下图的前序遍历顺序为：ABDGHCEIF。

    /**
     * 递归前序遍历
     *
     * @param node
     */
    public void preOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        System.out.print(node);
        preOrder(node.left);
        preOrder(node.right);
    }

    /**
     * 非递归前序遍历
     *
     * @param node
     */
    public void noRecursionPreOrder(TreeNode node) {
        if (node != null) {
            Stack<TreeNode> stack = new Stack<TreeNode>();
            stack.add(node);
            while (!stack.isEmpty()) {
                node = stack.pop();
                System.out.print(node);
                if (node.right != null) {
                    stack.push(node.right);
                }
                if (node.left != null) {
                    stack.push(node.left);
                }
            }
        }
    }

中序遍历

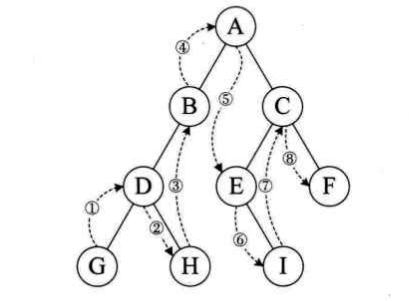
规则：若树为空，则空操作返回；否则从根结点开始（并不是先访问根结点），中序遍历根结点的左子树，然后访问根结点，最后中序遍历右子树。如下图的中序遍历顺序为：GDHBAEICF。

    /**
     * 递归中序遍历
     */
    public void inOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        inOrder(node.left);
        System.out.print(node);
        inOrder(node.right);
    }

    /**
     * 非递归中序遍历
     *
     * @param node
     */
    public void noRecursionInOrder(TreeNode node) {
        if (node != null) {
            Stack<TreeNode> stack = new Stack<>();
            while (!stack.isEmpty() || node != null) {
                if (node != null) {
                    stack.push(node);
                    node = node.left;
                } else {
                    node = stack.pop();
                    System.out.print(node);
                    node = node.right;
                }
            }
        }
    }

后序遍历

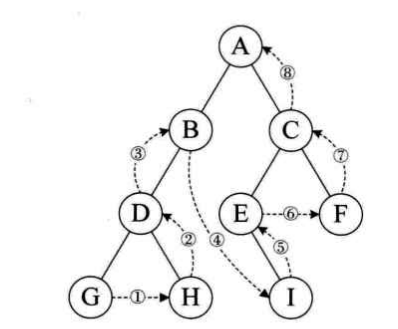
规则：若树为空，则空操作返回；否则从做到有先叶子后结点的方式遍历访问左右子树，最后访问根结点。如下图的后序遍历顺序为：GHDBIEFCA。

    /**
     * 递归后序遍历
     *
     * @param node
     */
    public void postOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.print(node);
    }

    /**
     * 非递归后序遍历
     *
     * @param node
     */
    public void noRecursionPostOrder(TreeNode node) {
        if (node != null) {
            Stack<TreeNode> s1 = new Stack<>();
            Stack<TreeNode> s2 = new Stack<>();
            s1.push(node);
            while (!s1.isEmpty()) {
                node = s1.pop(); // 头 右 左
                s2.push(node);
                if (node.left != null) {
                    s1.push(node.left);
                }
                if (node.right != null) {
                    s1.push(node.right);
                }
            }
            // 左 右 头
            while (!s2.isEmpty()) {
                System.out.print(s2.pop());
            }
        }
    }

层序遍历

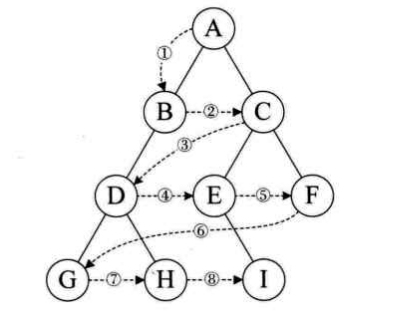
规则：若树为空，则空操作返回；否则从数的第一层，也就是根结点开始访问，从上往下逐层遍历，在同一层中按从左到右的顺序对结点逐个访问。如下图的层序遍历顺序为：ABCDEFGHI。

    /**
     * 层序遍历
     *
     * @param node
     */
    public static void level(TreeNode node) {
        if (node == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(node);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.println(cur);
            if (cur.left != null) {
                queue.add(cur.left);
            }
            if (cur.right != null) {
                queue.add(cur.right);
            }
        }
    }