概念

二叉树（Binary Tree）是 n（n≥0）个结点的有限集合，该集合或者为空（称为空二叉树），或者由一个根结点和两棵互不相交的、分为称为根结点的左子树和右子树的二叉树组成。

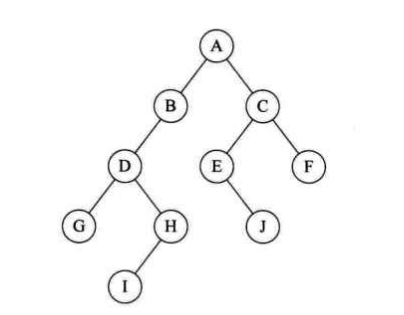
二叉树的特点：

• 每个结点最多有两棵子树，所以二叉树不存在度大于 2 的结点。没有子树或只有一棵子树也是可以的。
• 左子树和右子树是有顺序的，次序不能颠倒。
• 即使某个结点只有一颗子树了，也要区分是左子树还是右子树。

二叉树的五种基本形态：

1. 空二叉树。
2. 只有一个根结点。
3. 根结点只有左子树。
4. 根结点只有右子树。
5. 根结点既有左子树又有右子树。

二叉树的性质

1. 在二叉树的第 i 层上至多有 2^(i-1)个结点（i ≥ 1）。
2. 深度为为 k 的二叉树至多有 2^k - 1 个结点（k ≥ 1）。
3. 对任何一个二叉树 T，如果其叶子结点数为 n0，度为 2 的结点数为 n2，则 n0 = n2 + 1。
4. 具有 n 个结点的完全二叉树的深度为 [log2n] + 1（[x]表示不大于 x 的最大整数）。
5. 如果对一棵有 n 个结点的完全二叉树（其深度为 [log2n] + 1）的结点按层序编号（从第 1 层到第 [log2n] + 1 层，每层从左往右），对任一结点 i（1≤ i ≤n）有：
   1. 如果 i = 1，则结点 i 是二叉树的根，无双亲；如果 i>1，则其双亲是结点 [i/2]。
   2. 如果 2i > n，则结点 i 无左孩子（结点 i 为叶子结点）；否则其左孩子是结点 2i。
   3. 如果 2i + 1 > n，则结点无右孩子；否则其右孩子是结点 2i + 1。

特殊二叉树

斜树

所有的结点都只有左子树的二叉树叫做左斜树。所有的结点都只有右子树的二叉树叫做右斜树。

左斜树示意：

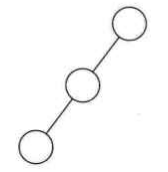
右斜树示意：

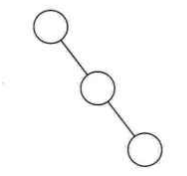
满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在统一层上，这样的二叉树称为满二叉树。

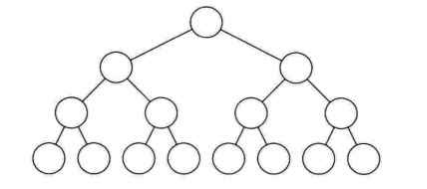
满二叉树的特点：

1. 叶子结点只能出现在最下一层，出现在不同层就不可能达到平衡。
2. 非叶子结点的度一定是 2。
3. 在同样深度的二叉树中，满二叉树的结点个数最多。

完全二叉树

对一棵具有 n 个结点的二叉树按层序编号，如果编号为 i（1≤ i ≤n）的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

通俗一点说就是，完全二叉树中的所有结点都是按照从上往下、从左往右的顺序依次排列，中间没有空缺的。满二叉树一定是完全二叉树，但是完全二叉树不一定是满二叉树。

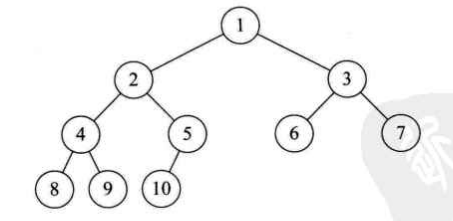
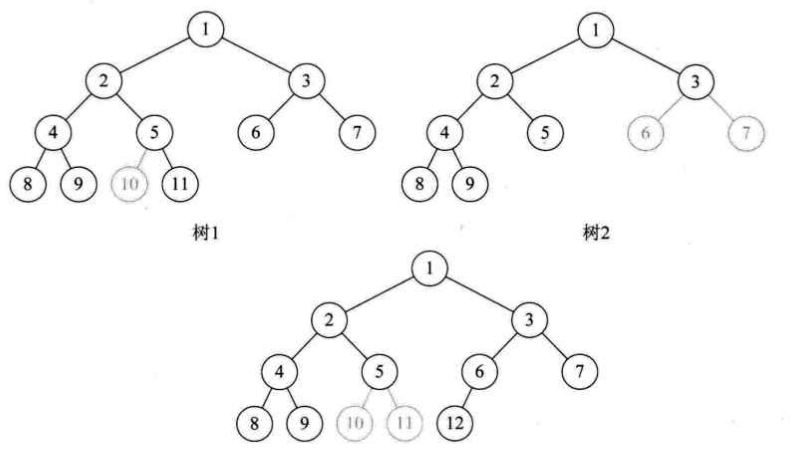
下图中展示的三棵树都不是完全二叉树，因为每棵树中的结点并未按照从上往下、从左往右依次排列的原则，中间均出现了空缺。

完全二叉树的特点：

1. 叶子结点只能出现在最下两层。
2. 最下层的叶子一定集中在左部连续位置。
3. 倒数第二层如果有叶子结点，一定是在右部连续位置。
4. 如果结点的度为 1，则该结点只有左孩子。
5. 同样结点数的二叉树，完全二叉树的深度最小。

二叉树的存储结构

顺序存储结构

由于二叉树是一种特殊的树，每个结点最多只有两个孩子结点，所以用顺序结果也是可以实现的。二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，也就是数组的下标要能体现结点之间的逻辑关系。

对于一棵二叉树 T：

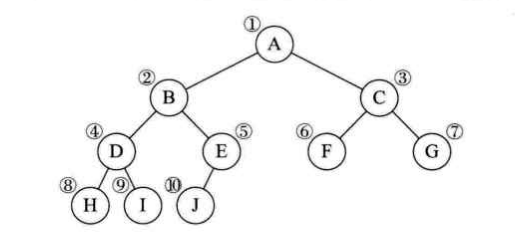
如果用数组表示，相应数组下标对应其相同的位置：

对于一般二叉树，可以将不存在的结点用特殊符号来标记，如：

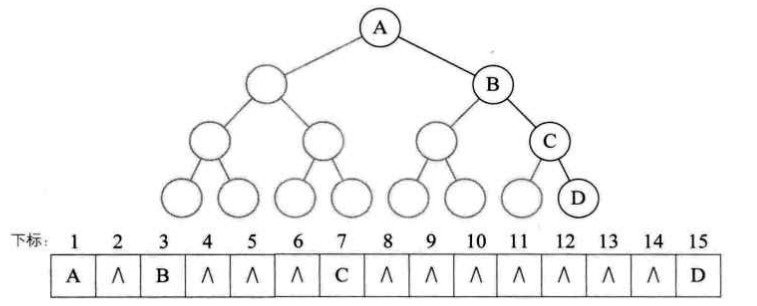
二叉链表

二叉树每个结点最多有两个孩子，那么利用链表来实现，链表中的每个结点有一个数据域和两个指针域，这种链表叫做二叉链表。

其中 data 是数据域，lchild 和 rchild 是分别指向左孩子和右孩子的指针域。