概念

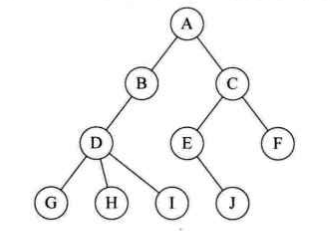
树（Tree）是 n（n ≥ 0）个结点的有限集。n = 0 时称为空树。在任意一棵非空树中：

1. 有且只有一个特定的称为根（Root）的结点；
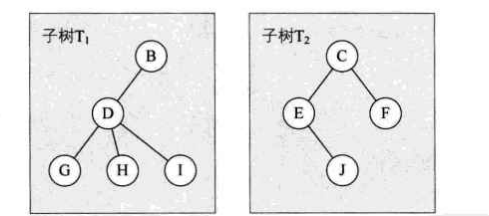
2. 当 n > 1 时，其余结点可分为 m（m > 0）个互不相交的有限集 T1、T2、......、Tm，其中每一个集合本身又是一棵树，并且称为根的子树（SubTree）。

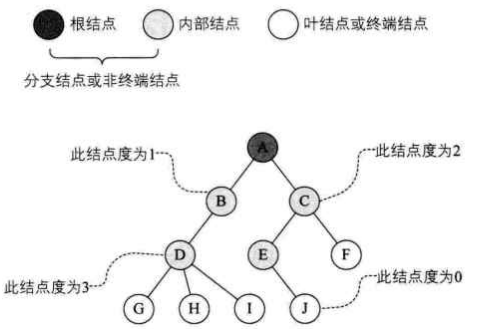
结点拥有的子树称为结点的度（Degree）。度为 0 的结点称为叶子结点（Leaf）或终端结点；度不为 0 的结点称为非终端结点或分支结点。除根结点外，分支结点也称为内部结点。树的度是树内各结点的度的最大值。

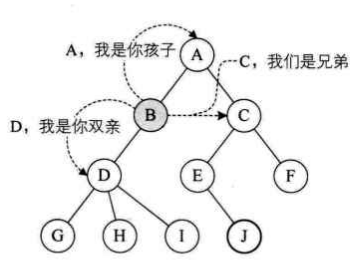
结点的子树的根称为该结点的孩子（Child），该结点称为孩子结点的双亲（Parent）。同一个双亲的孩子之间互称兄弟（Sibling）。结点的祖先是从根到该结点所经分支上的所有结点，如 D、B、A 都是 H 的祖先。以某结点为根的子树中任一结点都称为该结点的子孙，如 B 的子孙有 D、G、H、I。

结点的层次（Level）从根开始定义，根为第一层，根的孩子为第二层。双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度（Depth）或高度。

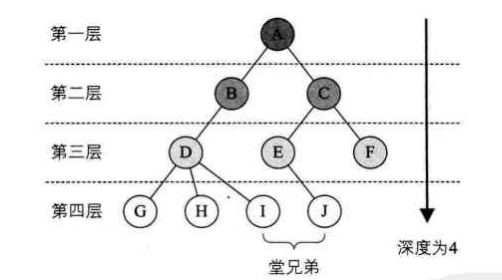
如果树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。

森林（Forest）是 m（m ≥ 0）棵互不相交的树的集合。

树的存储结构

双亲表示法

在每个结点中，附设一个指示器指示其双亲结点到链表中的位置。也就是说每个结点除了知道自己，还知道自己的双亲在哪里。

孩子表示法

每个结点有多个指针域，其中每个指针指向一棵子树的根结点，这种表示法叫做多重链表示法。但是由于每个结点的孩子个数不同，可以设计两种方案。

方案一：

指针域的个数就等于树的度。其中 data 是数据域，child1 到 childd 都是指针域。

但是这种方法对于树中各个结点的度相差很大时，会造成空间浪费，因为有很多结点的指针域都是空的。

方案二：

每个结点的指针域的个数就等于该结点的度，专门取一个位置来存储结点指针域的个数。

这种方式克服了浪费空间的缺点，但是由于各个结点的链表是不同的结构，加上要维护结点的度，所以会带来更加复杂的计算。

孩子兄弟表示法

任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右边的兄弟如果存在也是唯一的。因此，设置两个指针分别指向该结点的第一个孩子和其右兄弟。这种表示法可以称为孩子兄弟表示法。