概念

美国数学家 David Huffman（哈夫曼或赫夫曼）在 1952 年发明了哈夫曼编码，为了纪念他的成就，于是就把他在编码中用到的特殊二叉树称之为哈夫曼树。

在了解哈夫曼树之前，先了解一些哈夫曼树相关的其它术语：

• 路径：在一棵树中，从一个结点往下可以到达的孩子或孙子结点之间的通路称为路径。在下图中从根结点到结点 a 之间的通路就是一条路径。
• 路径长度：通路中分支的数目称之为路径长度。若规定根结点的层数为 1，则从根结点到第 L 层结点的路径长度为 L-1。下图中从根结点到结点 c 的路径长度为 3。
• 结点的权：若将树中结点赋给一个有某种含义的数值，则这个数值称为该结点的权。下图中结点 a 的权威 7，结点 b 的权威 5，结点 c 的权为 2。
• 结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。下图中结点 a 的带权路径长度为 1 * 7 = 7，结点 b 的带权路径长度为 2 * 5 = 10。
• 树的带权路径长度：所有叶子结点的带权路径长度之和，记作 WPL。下图中树的带权路径长度为 1 * 7 + 2 * 5 + 3 *2 + 3* 4 = 35。

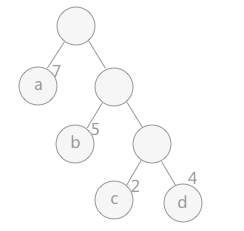
假设有 n 个权值{w1,w2,...,wn}，构造一棵有 n 个叶子结点的二叉树，每个叶子结点带权 wk，每个叶子的路径长度为 lk，则其中带权路径长度 WPL 最小的二叉树称作哈夫曼树，也称作最优二叉树。

构造哈夫曼树

1. 根据给定的 n 个权值{w1,w2,...,wn}构成 n 棵二叉树的集合，F = {T1,T2,...,Tn}，其中每棵二叉树 Ti 中只有一个带权为 wi 的根结点，其左右子树为空。
2. 在 F 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树根结点的权值之和。
3. 在 F 中删除这两棵树，同时将新得到的二叉树加入 F 中。
4. 重复步骤 2 和 3，直到 F 只含一棵树为止。这棵树就是哈夫曼树。

举个例子，假设有 a、b、c、d 四个结点，结点的权分别为 7、5、2、4，如下图：

找出现有权值中最小的两个结点 c 和 d 构造一棵新的二叉树，新二叉树的根结点的权值为 2 + 4 = 6，同时删除 c 和 d，得到下图：

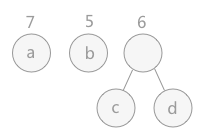
重复步骤 2 和 3 得到下图：

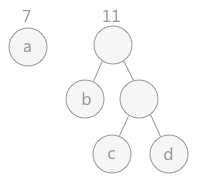
重复步骤 2 和 3，得到下图：

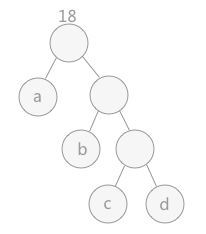
所有结点已经组成了一棵树，构造结束。